 |
| О клубе | Программы | Членство | Персоналии | English |
К.П.Бутусов. ДИСКРЕТНЫЕ СВОЙСТВА СОЛНЕЧНОЙ СИСТЕМЫ (окончание) |
|
Первая часть статьи Вторая часть статьи Логарифмическая дискретность радиусов орбит Как оказалось, кроме линейной дискретности, параметры грависистемы, рассмотренной выше, обладают еще специфической логарифмической дискретностью, то есть логарифмы радиусов орбит представляют собой дискретный! ряд, кратный минимальному значению. В табл. 7 приведены результаты этого расчета. 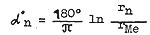 где rn - радиус n-й орбиты;  Из таблицы следует, что логарифмы радиусов орбит образуют дискретный ряд с ошибкой менее 4%. Анализ rpaвисистем с точки зрения принципов квантовой механики Как известно решение Шредингера для атома водорода ищут в виде степенного ряда: 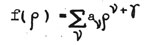 причем берут для γ значение γ=1 отбрасывая другое значение с тем, бы ряд не обращался в бесконечность при ρ =0. Однако для грависистемы характерно положение почти всей массы системы в состоянии с минимальной энергией, то есть в центральном теле, масса которого на много порядков больше образующих его частиц. Поэтому мы должны использовать второе значение γ= -( l +1) (3). Но тогда n и l будут связаны другим соотношением: n= - nr - l (4) вместо n= nr l +1 (5). Это ведет к тому, что тела, входящие в подсистему (по аналогии с оболочкой в атоме) могут иметь при данном l различные n < 1 , в то время, как в атоме
n > l+1. Плотность вероятности для нормального состояния в атоме водорода имеет сферическую симметрию, что характерно также для центрального тела грависистемы. Причем, ядро и оболочка, соответствующая наинизшему энергетическому уровню, в случае грависистемы не различимы в силу одноименности их зарядов. 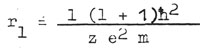 Тогда средняя орбитальная скорость будет приобретать значения  Если выразить скорость через ее максимальное значение, то получим: 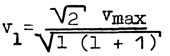 Максимально возможной средней скоростью у поверхности центрального тела для стационарного состояния является круговая скорость VI . Но, как известно, параболическая скорость 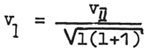 Как показывает расчет, орбитальные скорости холодных грависистем (систем спутников планет) неплохо описываются этой формулой. Покажем это на примере Юпитера (см. табл. 8). 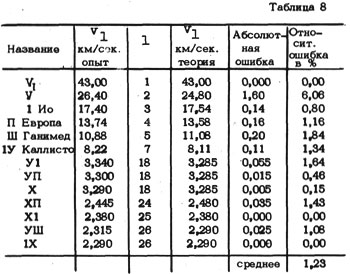 Как видно из таблицы, средняя ошибка, даваемая формулой, довольно мала (около 1%), что указывает, по-видимому, на правильность сделанных предположений.
Более глубокий анализ данного вопроса показывает что при вычислении стационарных значений орбитальных скоростей необходимо учитывать соотношение плотности спутника и центрального тела, при этом результаты теоретических расчетов еще лучше согласуются с экспериментом; ЛИТЕРАТУРА
|
|
© 2001-2026 Международный Клуб Учёных |
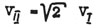 и поэтому формулу (8) можно записать в следующем виде:
и поэтому формулу (8) можно записать в следующем виде: