|
| О клубе | Программы | Членство | Персоналии | English |
К.П.Бутусов. СВОЙСТВА СИММЕТРИИ СОЛНЕЧНОЙ СИСТЕМЫ (окончание) |
|
Свойство спиральности Это свойство заключается в том, что перигелии и афелии планет лежат ва логарифмических спиралях. Математическое выражение для этого свойства выглядит так:
где π º n - долгота перигелия или афелия n-ой планеты, в градусах; Таблица 6 и рис.5 иллюстрируют эту закономерность. 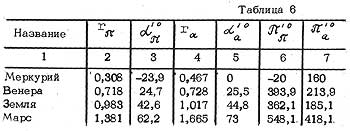 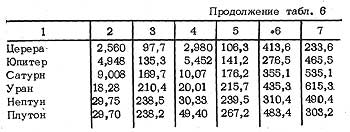 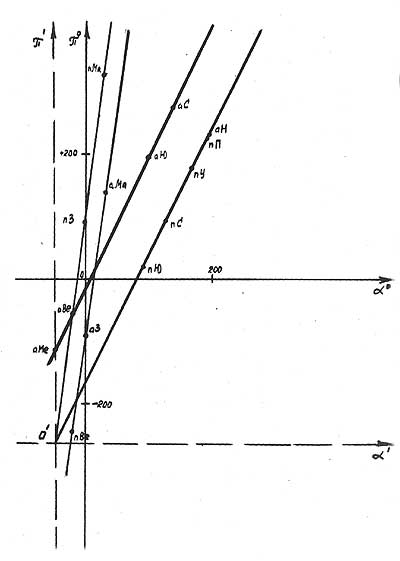 Рис. 5 Свойство спиральности.  угловые коэффициенты для спиралей: угловые коэффициенты для спиралей:K1= 8,4 ± 0,4 для первой, K2= 2,09 ± 0,01 для второй. Следует отметить, что перигелии и афелии Юпитера, Сатурна, Урана, Нептуна и Плутона лежат на одной пере спиралей с К=2, а афелии и перигелии Земли и Марса -на другой паре с К=8, однако, афелии Меркурия и Векеры принадлежат обеим парам спиралей. Свойство спиральнссти носит, по—видимому, более общий характер, т.к. известно, что спирали галактик тоже имеют логарифмический вид. Структурная диаграмма Как показал сравнительный анализ обнаруженных свойств симметрии, все они могут быть связаны единой геометрической схемой, названной автором структурной , диаграммой, причем, каждому свойству симметрии Солнечной системы соответствует определенный вид симметрии структурной диаграммы. 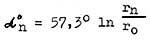 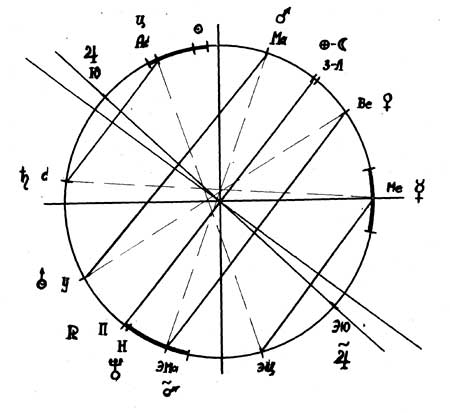 Рис. 6 Структурная диаграмма rn - средний радиус орбиты планеты -n r0 - средний радиус орбиты Меркурия, (n=0) rmin - радиус орбиты планеты n в перигелии Данные расчета сведены в таблицу 7. 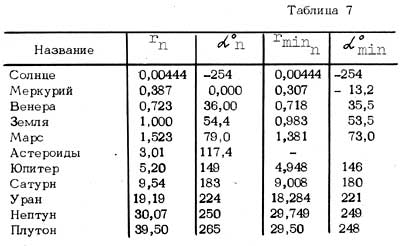 Поясу астероидов соответствует не точка, а дуга, на которой находится также Солнце. Полученная диаграмма симметрична относительно нескольких осей и центра. Каждому свойству симметрии соответствует своя ось или центр:
На основании обнаруженных закономерностей можно будет уточнить параметры одних тел и предсказать параметры других, еще нe открытых. В частности, из свойств симметрии следует наличие, как минимум, еще трех планет за Плутоном. В табл. 8 приведены их ориентировочные параметры. 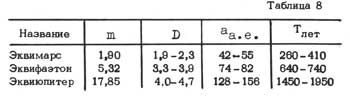 здесь m - масса, D - диаметр, а - большая полуось орбиты, Т - период обращения. Параметры Земли взяты за единицу. В работе приведены пока только эмпирические закономерности, но они, безусловно, отражают действие некоторых внутренних причин, определяющих взаимосвязь параметров тел Солнечной системы и общность их эволюции. Теория этих явлений в настоящее время разрабатывается автором и будет опубликована в последующих работах. Литература
|
|
© 2001-2026 Международный Клуб Учёных |
 Начало статьи
Начало статьи